TLDR; Experiment splitting can be an effective method to borrow strength across similar experiments and metrics to improve the performance of treatment effect estimators. Using data from 226 Facebook News Feed experiments, the paper shows that using a Lasso estimator based on experiment splitting would lead to substantially improved launch decisions.
It is common practice to launch new features based on standard treatment effect estimators obtained in A/B tests. Today’s paper is asking the question whether we can make better decisions if we have data from other related A/B tests available. It turns out we can!
Using a dataset of 226 Facebook News Feed A/B tests, we show that a lasso estimator based on repeated experiment splitting has a 44% lower mean squared predictive error than the conventional, unshrunk treatment effect estimator, a 18% lower mean squared predictive error than the James-Stein shrinkage estimator, and would lead to substantially improved launch decisions over both.
A Bayes Estimator for treatment effects
The average treatment effect is generally the object of interest in A/B tests. For a test i, we can define it as
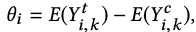
where the superscripts t and c are for treatment and control, k are the units/users and Y is the outcome of interest. The difference of sample means treatment effect estimator is
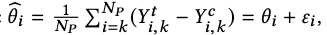
where epsilon is a mean zero independent sampling error.
We are interested in estimating the treatment effect by means of the Bayes estimator
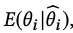
that minimises the mean squared error (MSE). The empirical Bayes literature is rich in approaches for estimating this quantity under various distributional assumptions, such as the James-Steines estimator or Tweedie’s formula. Commonly, those estimators perform well in terms of MSE as they shrink the parameters towards some prior mean, often as a function of the signal-to-noise ratio. While those estimators can already improve over standard treatment effect estimators by borrowing strength across different experiments, this paper goes further and explores estimators based on experiment splitting.
Experiment Splitting – Partitioning experiments into sub-experiments
The main observation is that multiple independent estimates of the same treatment effect can be obtained from a single experiment, by simply partitioning the experiment into subexperiments. In brief, by randomly splitting each experiment into two subexperiments, we can estimate the conditional mean of the treatment effect estimate in the second subexperiment given the treatment effect estimate in the first. This conditional mean is what is required for optimally shrinking our estimates from the second subexperiment.
Experiment splitting essentially gives us two treatment effect estimators for each experiment ![]() and
and ![]() , from which we estimate
, from which we estimate
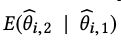
using any appropriate method, such as linear regression. Assuming ![]() equals the previously defined treatment effect plus an independent sampling error, it holds that
equals the previously defined treatment effect plus an independent sampling error, it holds that
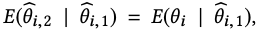
which is the Bayes estimator of the treatment effect conditional on the information obtained from the first experiment. In relation to terminology used in Machine Learning, the authors call the first sub-experiment training experiment and the second experiment validation experiment.
While not conditioning on all the information might impair estimator performance, the paper indicates that the gain from being able to shrink outweighs the potential loss due to not conditioning on all the information in empirical applications.
A nice side effect is that the approach extends to any set of conditioning variables X so we can estimate
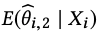
In this equation, X contains an estimate from the treatment effect in the first experiment and all other variables deemed predictive of the for the treatment effect, such as the treatment effect of other metrics in the same experiment. It can be estimated by standard algorithms, such as the Lasso or neural nets.
Selecting the optimal experiment splitting fraction
Given we need to partition a single experiment into two experiments and this split affects the properties of the estimator though the impact of the sampling error in the estimates, the question is how to optimally do that?
One approach outlined in the paper is cross-validation using minimal prediction error on a test set as a criterion. The algorithm is defined as follows (gamma is the splitting fraction – the share of units selected for the training sub-experiment):

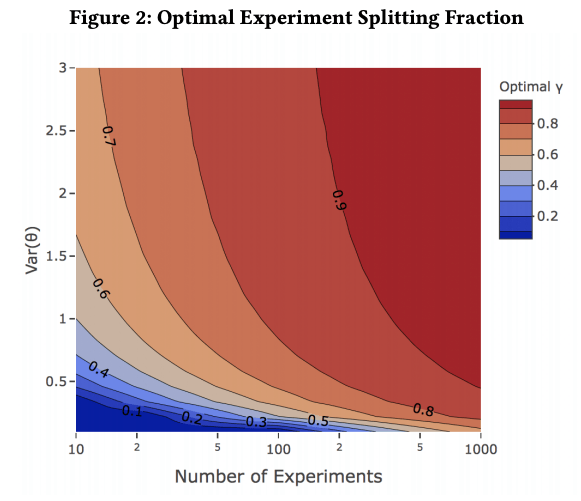
For the case of univariate OLS, where we regress the estimated treatment effect of the validation experiment on the estimated treatment effect in the training experiment and a constant, Figure 2 below shows how the optimal splitting fraction depends on the number of experiments and the variance of the treatment effects for a fixed sampling error. The figure indicates a higher treatment effect variance requires a larger share of units to be assigned to the training experiment.
Improving estimators for Facebook News Feed experiments
To validate the approach, the authors study a set of 226 Facebook News Feed A/B tests conducted in 2018. The A/B tests caused a change in the order in which stories appear on the news feed. They evaluated experiment splitting estimators against pooled estimators (that is, estimators not using splitting) using the squared distance criterion on a test set.
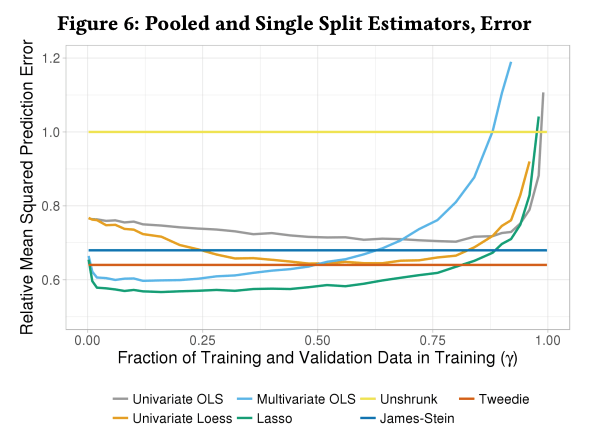
Figure 6 shows the prediction error of pooled estimators (Unshrunk, James-Stein, Tweedie) and experiment splitting estimators. The unshrunk estimator is essentially the commonly used difference in sample means estimator. It turns out the experiment splitting Lasso estimator substantially outperforms all other estimators, at least when the optimal splitting fraction is selected. To compute it, the authors use the percentage change in all metrics (24 in total) in the training experiment as predictors. The same set of predictors is used in multivariate OLS, whereas univariate OLS only uses the outcome variable as predictor.
Since the mean squared prediction error is generally not the business relevant outcome, the authors infer that launching all experiments with a positive estimated treatment effect gives a cumulative uplift in the business metric of 11.2 % when using the unshrunk estimator vs. 15.7 % when using the Lasso.
Related to the predictors used, the paper also has something very interesting to say about borrowing strength not only from other experiments, but from other metrics that correlate with the outcome of interest:
Indeed, the multivariate OLS and lasso estimators perform well. At their optimal splitting fractions they improve on the unshrunk estimator by 40% and 43%, and on Tweedie by 7% and 11%. This implies that our inferences about changes in posts can be much improved by taking into account how other metrics have changed, because of the correlation between the true treatment effects for posts and for other metrics. Thus experimental analyses which analyze one metric in isolation, without taking into account the comovements in other, related metrics may be quite suboptimal.