Position Ranking and Auctions for Online Marketplaces

Position Ranking and Auctions for Online Marketplaces, Chu et. al., Management Science, 2020

The January issue of Management Science has a very impressive paper about optimal position ranking under information asymmetry. It is impressive because (a) it exactly models the problem many marketplaces – especially those selling physical goods – are facing and (b) it covers the problem holistically and in great depth, taking different optimisation objectives as well as asymmetric information into account.

Online e-commerce platforms, such as Amazon and Taobao, connect thousands of sellers and consumers every day. In this work, we study how such platforms should rank products displayed to consumers and utilize the top and most salient slots.

Besides deriving an optimal ranking strategy, the paper

• offers a theoretical motivation for running sponsored search systems, as in the model they vastly increase efficiency arising from information asymmetries on the supply side between sellers and the platform,

That is, the platform may be unaware of the private benefits to sellers’ of each consumer purchase—for example, profits, brand effects, and so on. We demonstrate that making an uninformed ranking decision can lead to a large loss of surplus to the platform, especially when
the number of items is large.

• shows how to optimise for multiple objectives, including the welfare of consumers and product suppliers and
• explicitly models the consumer choice problem when examining ranked products using a model with behavioural implications that mimic empirical results on actual product examination behaviors.

The key model ingredients are a sequential search model on the demand side and a optimisation model under information asymmetries on the supply side. Compared to most of the previous literature, the consumer side model in the paper leads to click probabilities that are not multiplicatively separable in a position and relevance part, as showing a highly relevant item on top under the model will lead to a lower click probably for longer ranked items independent of their relevance and the position.

Key results of the paper are (i) without information asymmetries, the optimal ranking function when considering welfare and revenue has a simple structure and is a weighted function of sellers welfare/margins, price and a term balancing consumer utility and search costs and (ii) with incomplete information the ranking function – now with unknown seller utility – can be implemented in incentive-compatible dominant strategies.

Sequentially searching consumers, sellers with private information and a platform with long-term objectives

The demand side model is motivated by the empirical observation that most consumers examine result sets sequentially and has two parts: The utility a consumer obtains from a purchase and the search costs of finding the purchase. The utility from purchase for consumer i is

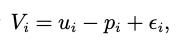
where u is the direct utility from product the product, p is price and epsilon is a random component.

When examining the ranking, the consumer decides whether to examine the next item or purchase the current item and leave. She will purchase and leave if her current best utility for all the examined items is higher than the expected utility of examining more items. Let v_* be the solution to

where s are the cost of examining the next item, v is the current best utility and V is a random utility of the next item and the right hand side reflects the expected utility of examining one more item, which might be worse (first term) or better (second term) than the current best item. Then, she will continue examining until she first views an item with utility higher than v_*. The following lemma summaries consumer behaviour. Not that the consumer can obtain (random) value V_0 when not searching (outside option).

Hence, demand for an item can either come from consumers seeing an item and purchasing (called “fresh demand” in the paper) or from consumers examining all items and the making a purchase (“returned demand”). “Returned demand” is independent of the ranking, while “fresh demand” depends on it.

Sellers on the platform have, potentially private, valuations theta from selling an item. The platform’s goal is to maximise the synthesis of consumer surplus, aggregate platform revenue and supply side surplus by selecting a ranking. Conceptually, it maximises the following weighted surplus function

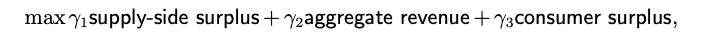
What optimises the platform’s weighted surplus?

The paper shows how to optimise weighted surplus first under the assumption the platform knows everything and then considers the case of incomplete information about the utility/profit of sellers. Under complete information, the ranking is a rather simple (weighted) function of the utility of sellers, price and a term balancing expected utility given purchase and normalised search costs.

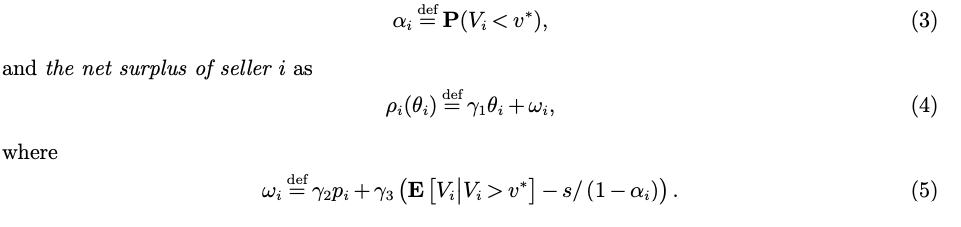
where theta is the utility of a seller.

Now, how big of an issue it is for the platform to use a ranking without knowing sellers’ private utility? The model says it is a big issue.

We first reveal a notable gap between the weighted surplus from the optimal ranking with incomplete information and from that with complete information in Section 4.1. We show that, as the number of sellers in the market increases, the average surplus loss in the worst case can be arbitrarily bad. Following this discussion, motivated by the sponsored search practices, in Section 4.2 we propose the remedy: selling the top few slots using the surplus-ordered ranking (SOR) mechanism.

Prior to 2012, Amazon only presented organic search results, and no positions were auctioned off. For such an uninformed ranking, Propositions 1 and 3 imply substantial room for improvement.

Maximising surplus under incomplete information

To maximise surplus under incomplete information, the platform may decide to sell k slots via a sponsored search program. The questions then are how to allocate items (allocation rule) and how to construct payments (payment rule)?

The result of the paper is in a nutshell that weighted surplus is maximal when the platform uses net surplus as defined above for the top k slots (assuming knowledge of sellers’ utility) and the base order (the platform’s off-the-shelf-ranking without the sponsored search system) for the remaining slots as an allocation rule and implement a mechanism to truthfully elicit sellers’ utility.

The authors show allocations are monotone in seller’s valuations and construct the payment rule using Myerson (1981). An interesting twist is that, due to externalities and slot restrictions, the VCG mechanism would require payments from items not allocated to the top k slots and hence can’t be implemented. The paper hence designs a different incentive-compatible mechanism.

We show that our mechanism is near-optimal, performing significantly better than those that do not incentivize the sellers to reveal their private information.