Optimal Auctions through Deep Learning

Optimal Auctions through Deep Learning, Dütting et al., 2019

How to design a revenue maximising and incentive compatible auction in settings where we do not know how to explicitly characterise the allocation and payment functions? Or, more the point, how to design such auctions for most real world applications? Today’s paper proposes neural networks to solve this challenge.

The paper is one more piece in the fascinating literature on automated mechanism design that applies machine learning techniques to market design questions. In the domain of auctions, this has huge potential precisely because designing incentive compatible auctions that maximise expected revenue is an intricate task and – despite the practical importance of this problem – little is known beyond the case where are single item is for sale.

The single-item case was resolved in a seminal piece of work by Myerson in 1981. Even after 30-40 years of intense research the problem remains unsolved for seemingly simple multibidder, multi-item settings.

Incentives, efficiency and revenue – we can’t have all at once

Three desirable properties of auctions are

• Dominant strategy incentive compatibility (DSIC): For all bidders, regardless of the actions of other bidders, it is never beneficial for the bidder to bid something other than her value.
• Efficiency: The items are allocated to maximise social welfare. In particular, items change hands if there is a bidder with positive valuation (and the auctioneer has zero value for the objects).
• Revenue-maximising: The auction maximises the revenue for the auctioneer.

Theory tells us we can’t have all of them at the same time. We generally have to sacrifice one of them. Which one to sacrifice is usually guided by the business context. For example, in ad auctions, efficiency is generally not a concern, but revenue and incentives matter. In government auctions, the focus is often on incentives and efficiency. When designing for incentives and efficiency, the VCG mechanism is the obvious choice and a lot is known about how to characterise VCGs in different environments. However, when designing for DSIC and maximal revenue, very little is known beyond simple and special cases. This is the starting point of today’s paper.

In this work we provide the first, general purpose, end-to-end approach for solving the multi-item (optimal) auction design problem.

Compared to earlier work on automated auction design which searches for optimal auctions directly in the space of incentive compatible ones, Sandholm and Likhodedov (2015) being an example, the methods in this paper do not impose any a priori equilibrium restrictions and search in a larger space of auctions, aiming at finding the one that is revenue maximal and DSIC rather than finding the revenue maximal auction among the DSIC auctions.

Learning optimal auctions with neural nets

One of the main innovations of the paper is to cast the optimal auction design problem as a learning problem. The authors formulate an optimisation problem over a neural network, optimise and train the network and recover the optimal auction design for cases where solutions are known. Using the approach, they are able to

• recover – up to some error – essentially all analytical solutions to the optimal auction design problem that have been obtained over the last 30-40 years,
• find high-revenue auctions for situations in which the optimal auction design is not known and
• are able to learn for larger settings, such as 5 bidders and 10 auctions.

The paper also contains generalisation bounds to tie training outcomes to outcomes on new samples.

The optimal auction learning problem

The optimal auction design problem is formulated as an expected revenue maximisation (expected negative revenue minimisation) problem subject to a no ex post regret constraint. The no ex post regret constraint ensures no bidder can benefit from not bidding truthful, and hence ensures DSIC.

In the above equation, w are (neural network) parameters indexing the space of all auctions, v are (exogenous) valuations, p are payments, rgt is ex post regret and i reflects the identity of bidders. The empirical version of the minimisation problem is

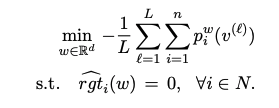
Neural networks for auction modelling

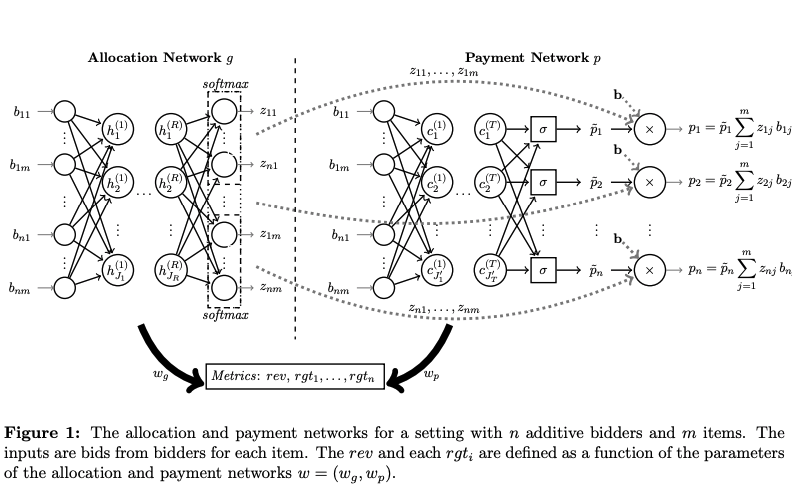
The figure above shows the allocation and payment neural network architectures for the case when bidders have additive valuations, that is, their value of a bundle of items is just the sum of the individual items in the bundle. The input layer of both networks accept bids. The allocation network outputs allocation probabilities, the payment network gives payments – both for the particular bid profiles.

The constrained optimisation problem is solved using the Lagrangian with a quadratic penalty for violating the constraints.

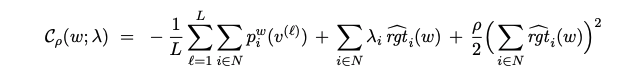
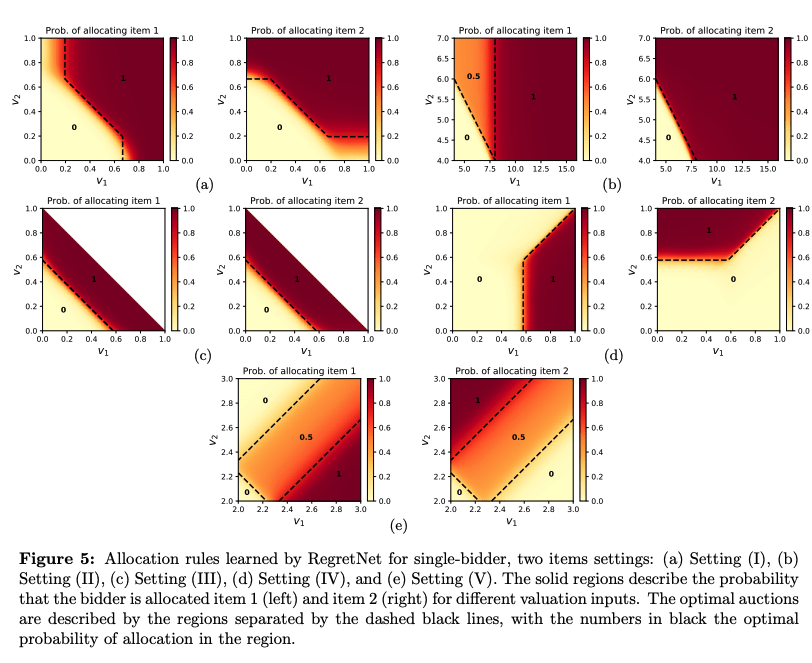
Experiments to recover optimal auctions

Implementing the learning algorithm in TensorFlow, the optimal auctions can be recovered with high accuracy for almost all cases where the optimal auction is known analytically. The figure shows the learned and theoretically optimal allocation rule for different settings, starting with a single bidder with uniform valuation over two items (Setting I) and ending with a single bidder with unit demand valuations drawn from a Uniform(2,3)-distribution (Setting V).

Final thoughts

Automated auction design has the potential to solve relevant economic design problems that remain unresolved since many years. While results from the paper are very promising, there are remaining challenges. First, the optimisation problems are generally not convex and thus are not guaranteed to achieve a global maximum. Second, even for small environments with a few bidders and items, training is costly and time consuming.

We envision progress at scale will come through (…) additional innovations in network architecture and in regard to methods to minimize ex post regret during training.